標準偏差とは？σの意味から計算方法・活用例までわかりやすく解説

標準偏差とは、データの「ばらつき」や「安定性」を数値で表す統計指標です。

平均値だけでは見えない、結果の一貫性や信頼性を客観的に判断するための基礎となります。

この記事では、標準偏差の意味・σ（シグマ）の由来・実際の計算方法・Excelでの求め方・日常やビジネスでの活用例までをやさしく解説します。

数学が苦手でも大丈夫です。

標準偏差を理解すれば、「平均」だけでは分からないデータの真実が見えるようになります。

数字の背景を読み解き、信頼できる分析を行うための第一歩として、この記事をぜひ参考にしてください。

標準偏差とは？意味をやさしく理解しよう
1. 標準偏差の基本定義と役割
2. 平均値では見えない「ばらつき」を数値化する理由
「σ（シグマ）」とは？標準偏差を表す記号の意味
1. σの読み方と由来
2. 平均値μとの関係を正規分布でイメージする
標準偏差の求め方をわかりやすく解説
標準偏差の単位と数値の読み取り方
標準偏差の実生活・ビジネスでの活用事例
標準偏差に関するよくある質問（Q&A）
まとめ｜標準偏差を理解してデータの「信頼性」を見抜こう

標準偏差とは？意味をやさしく理解しよう

この章では、「標準偏差とは何か？」という基本から、その役割や意味を初心者にもわかりやすく解説します。

平均値だけでは分からないデータの「ばらつき」をどう数値化するのかを理解することが、データ分析の第一歩です。

標準偏差の基本定義と役割

標準偏差（standard deviation）とは、データのばらつきを数値で表した統計指標です。

平均値だけでは見えない「データの散らばり具合」や「安定性」を定量的に把握できるのが特徴です。

たとえば、テストの平均点が同じクラスが2つあっても、点数の分布が違う場合があります。

Aクラスは全員が80点前後なのに対し、Bクラスは50点〜100点と幅広い点数を取っているとすれば、そのばらつきの度合いを示すのが標準偏差です。

標準偏差が小さいほどデータが平均値の近くに集まり、安定していることを意味します。

逆に大きい標準偏差は、データが広く散らばっており変動が大きい状態を示します。

標準偏差の大きさ	データの特徴
小さい	データが平均値付近に集中しており安定
大きい	データのばらつきが大きく不安定

平均値では見えない「ばらつき」を数値化する理由

平均値はデータの中心を示すだけで、実際にどれくらいの差があるのかまでは分かりません。

標準偏差を使えば、データが平均値の周りにどのように分布しているかを定量的に把握できます。

この「ばらつき」の数値化により、データの信頼性や安定性を客観的に判断できるのです。

たとえば、商品の月別売上データを分析する際、平均売上だけでなく標準偏差も確認することで、「安定して売れているのか」「波が大きいのか」を明確に判断できます。

標準偏差を理解することは、数字の裏にある“安定性”を読む力を身につけることにつながります。

「σ（シグマ）」とは？標準偏差を表す記号の意味

この章では、標準偏差を表す記号「σ（シグマ）」の意味と、平均値との関係をわかりやすく解説します。

記号の由来や使われ方を理解することで、統計式を読む力がぐっと上がります。

σの読み方と由来

σ（シグマ）は、標準偏差を表すために使われるギリシャ文字です。

大文字の「Σ（シグマ）」は「総和」を意味し、複数の数値を足し合わせる記号として使われます。

一方、小文字の「σ」は、その合計から派生し、「データのばらつき」を意味するようになりました。

つまり、「Σ」は全体の合計、「σ」はその中の散らばり具合を示す記号なのです。

記号	意味
Σ（シグマ）	合計を表す
σ（シグマ）	標準偏差（ばらつき）を表す

「σ」は“安定性の尺度”を象徴する記号として、統計学全般で広く使われています。

平均値μとの関係を正規分布でイメージする

統計分析では、平均値を「μ（ミュー）」、標準偏差を「σ（シグマ）」で表します。

平均値はデータの中心、σはその中心からどれだけ離れているかを示す指標です。

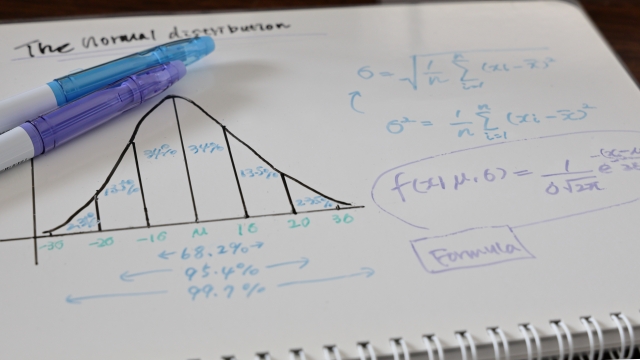
正規分布（ベルカーブ）を想像すると理解しやすく、±1σで約68％、±2σで約95％、±3σで約99.7％のデータが収まるとされています。

範囲	データの割合	意味
μ ± 1σ	約68%	大半のデータが収まる
μ ± 2σ	約95%	ほとんどのデータが含まれる
μ ± 3σ	約99.7%	外れ値を除いたほぼ全データ

この分布関係を理解しておくと、「標準偏差がどれくらい大きければ異常なのか」を直感的に判断できます。

3σルールと呼ばれる基準では、平均から±3σを超えるデータは異常値と見なされます。

このルールは、品質管理やリスク分析など、多くの業界で使われる重要な考え方です。

標準偏差の求め方をわかりやすく解説

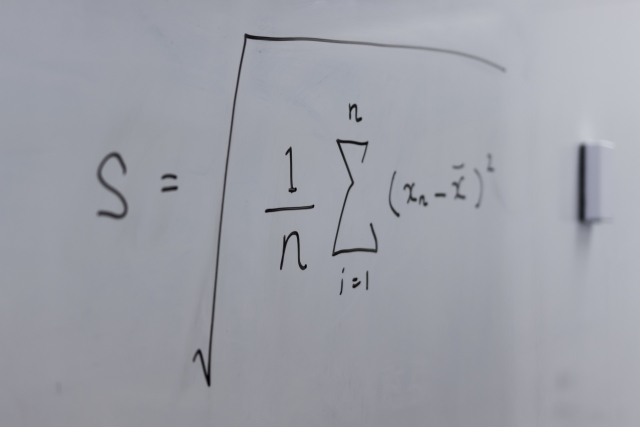
この章では、標準偏差の計算方法をステップごとに解説します。

手計算での理解を深めつつ、Excel関数を使って効率的に求める方法も紹介します。

手計算での標準偏差の計算手順

標準偏差は「データが平均値からどれだけ離れているか」を数値化したものです。

次の5つのステップを踏めば、誰でも求めることができます。

ステップ	手順	説明
①	平均値（μ）を求める	全データの合計をデータ数で割る。
②	偏差を求める	各データから平均値を引く。
③	偏差を二乗する	負の数をなくすために二乗する。
④	分散を求める	二乗の平均を取る。
⑤	平方根を取る	分散の平方根を取ると標準偏差が求まる。

たとえば、データが「2, 4, 4, 4, 5, 5, 7, 9」の場合、平均値は5、分散は4、標準偏差は2になります。

標準偏差＝ √(分散)という関係を覚えておくと、計算の流れが理解しやすくなります。

Excel関数で自動計算する方法

実務ではExcelを使えば、標準偏差を一瞬で求めることができます。

Excelには2種類の関数が用意されており、データの種類によって使い分けます。

関数名	用途	使用例
=STDEV.P(範囲)	母集団全体の標準偏差を求める	=STDEV.P(A1:A10)
=STDEV.S(範囲)	標本（サンプル）の標準偏差を求める	=STDEV.S(A1:A10)

さらに、グラフに「誤差範囲（エラーバー）」を追加すると、標準偏差を視覚的に確認できます。

平均値だけでは見えない安定性を見極めるのに最適です。

母集団と標本の違いに注意しよう

標準偏差を使うときに重要なのが、「母集団」と「標本」の区別です。

すべてのデータを扱う場合は母標準偏差（STDEV.P）を使い、サンプルデータで全体を推定する場合は不偏標準偏差（STDEV.S）を使います。

種類	分母	Excel関数	用途
母標準偏差	n	STDEV.P	全データを扱う場合
不偏標準偏差	n−1	STDEV.S	サンプルから推定する場合

母集団か標本かを区別することが、正しい分析の第一歩です。

標準偏差の単位と数値の読み取り方

この章では、標準偏差の「単位」と「数値の意味」を理解し、結果の読み取り方を学びます。

同じ数値でも単位や文脈が異なると意味が変わるため、正しい解釈が重要です。

なぜ標準偏差の単位は元データと同じになるのか

分散は偏差（二乗）の平均なので、単位が二乗になります。

たとえばデータの単位がcmであれば、分散の単位はcm²です。

しかし、標準偏差は分散の平方根を取るため、単位が元に戻り、直感的に理解しやすくなります。

指標	単位	特徴
分散	元データの単位²	理論的だが直感的ではない
標準偏差	元データと同じ単位	現実的で理解しやすい

この性質により、標準偏差は現実的な感覚で「平均からのズレ」を把握できます。

値が大きい・小さい場合の意味を比較する

標準偏差の大きさは、データの安定性や信頼性を示します。

値が小さいほどデータが平均に集中し、再現性が高い状態です。

標準偏差の大きさ	意味	例
小さい（例：1以下）	安定しており信頼性が高い	製品の品質が一定
中程度（例：2〜3）	やや変動があるが通常範囲	季節変動や自然な差
大きい（例：5以上）	変動が激しく不安定	市場や気候の影響が強い

標準偏差が小さいほど「安定している」と覚えておくと、ビジネスや教育分析でも役立ちます。

平均値との関係から「安定性」を判断する

平均値と標準偏差はセットで見ることで、データの信頼性を評価できます。

平均が高くても標準偏差が大きければ、ばらつきが大きく不安定な状態です。

逆に、平均が低くても標準偏差が小さければ、安定した結果を示しています。

平均値	標準偏差	解釈
高い	小さい	良好で安定した状態
高い	大きい	結果は良いがばらつき大
低い	小さい	安定しているが改善の余地あり

平均値だけではなく標準偏差も見ることで、より深い洞察が得られます。

標準偏差の実生活・ビジネスでの活用事例

この章では、標準偏差がどのように私たちの日常やビジネスの中で役立っているのかを紹介します。

数字を分析する力は、単なる数学の知識ではなく、実践的な判断力につながります。

売上やアクセス解析などビジネスデータへの応用

ビジネスの世界では、売上やアクセス数、顧客満足度などの数値が常に変動します。

その「安定度」を測るために使われるのが標準偏差です。

売上パターン	標準偏差	解釈
毎月ほぼ一定	小さい（1〜2）	安定した市場・リスクが小さい
季節変動あり	中程度（3〜5）	通常の範囲・改善可能
月ごとに大きく変動	大きい（6以上）	不安定・要対策

たとえば、ECサイトの売上を分析するとき、平均値だけを見ても本当の状態は分かりません。

標準偏差が小さいほど、経営の安定性が高いと判断できます。

逆に標準偏差が大きければ、シーズン要因やキャンペーン効果など外部要因を分析する必要があります。

教育現場での学力分析と偏差値の関係

教育分野では、テスト結果のばらつきを理解するために標準偏差が使われます。

平均点が同じでも、標準偏差によってクラス全体の理解度の差を把握できます。

標準偏差が小さい場合は、生徒全員の理解度が均一。

一方、標準偏差が大きい場合は、得点差が広く、理解度にばらつきがあることを意味します。

標準偏差	クラスの特徴	指導方針
小さい	全体的に均一	共通理解を前提に発展的内容へ
大きい	個人差が大きい	個別指導・補習が有効

さらに、入試や模試でよく使われる「偏差値」も標準偏差を基にしています。

偏差値は、個人の得点が平均値からどの程度離れているかを示す数値で、教育評価の基本となっています。

標準偏差を理解すれば、成績データを客観的に評価できるようになります。

品質管理・リスク評価での具体的な使われ方

製造業や品質管理の現場では、標準偏差は欠かせない指標です。

製品サイズのばらつきを±3σの範囲内に保つことで、品質の一貫性を保証します。

用途	目的	効果
製造業	製品寸法の安定管理	不良率の低減・コスト削減
金融業	価格変動リスク（ボラティリティ）測定	投資判断の基準化
医療・研究	測定データのばらつき確認	実験結果の信頼性向上

特に「3σルール」は、品質管理の国際的な基準であり、製品の約99.7％を平均値から±3σ以内に収めることを目標としています。

標準偏差は、あらゆる分野で「安定性」を測る共通の物差しとして機能しています。

標準偏差に関するよくある質問（Q&A）

最後に、標準偏差に関してよく寄せられる質問をまとめました。

初心者がつまずきやすいポイントを中心に、実務での使い方をわかりやすく整理しています。

標準偏差が1に近いときの意味

標準偏差が1に近いということは、データが平均値の近くに集まっていることを示します。

つまり、結果が安定しており、再現性が高い状態です。

標準偏差の値	データの特徴	判断
1以下	ばらつきが小さい	信頼性が高い
2〜3	中程度の変動	許容範囲内
4以上	大きな変動	外れ値や誤差を確認

標準偏差が1に近い＝安定していると覚えておくと良いでしょう。

不偏標準偏差と母標準偏差の違い

不偏標準偏差は、サンプル（標本）データから母集団全体を推定する際に使う補正付きの標準偏差です。

母標準偏差は全データを対象に計算するため、分母が異なります。

種類	分母	Excel関数	使用目的
母標準偏差	n	STDEV.P	全データを扱うとき
不偏標準偏差	n−1	STDEV.S	サンプルから推定するとき

データがサンプルか全体かを判断して関数を選びましょう。

σ（シグマ）の考え方を理解するメリット

σ（シグマ）を理解すると、データの信頼性やリスクを数値で説明できるようになります。

特に、正規分布では「平均値±1σ」に約68％、「±2σ」に約95％のデータが含まれます。

これを利用すれば、異常値やリスクの度合いを客観的に評価できます。

範囲	含まれるデータの割合	意味
μ ± 1σ	約68%	通常の範囲
μ ± 2σ	約95%	ほとんどのデータが収まる
μ ± 3σ	約99.7%	異常値を除いた範囲

σの理解＝「データを科学的に読む力」を意味します。

この考え方を身につけることで、感覚ではなくデータで判断できるようになります。

まとめ｜標準偏差を理解してデータの「信頼性」を見抜こう

ここまで、標準偏差の意味や計算方法、そして実生活やビジネスでの活用例を解説してきました。

最後に、この記事のポイントを整理して振り返りましょう。

ポイント	内容
標準偏差の基本	データのばらつきを数値化する統計指標であり、平均値だけでは見えない「安定性」を可視化できる。
σ（シグマ）の意味	標準偏差を表す記号で、データの散らばりを定量的に示す。
計算方法	分散の平方根を取ることで求められ、Excelでも簡単に計算できる。
単位と数値の解釈	標準偏差の単位は元データと同じであり、値が小さいほどデータが安定していることを意味する。
活用例	ビジネス・教育・品質管理などで「安定性」「信頼性」「リスク評価」を判断する指標として用いられる。